Banyak pecinta musik ingin download lagu di SoundCloud. SoundCloud adalah salah satu platform terbaik layanan streaming musik terpopuler. Kamu dapat mengunggah musik kamu sendiri di SoundCloud secara gratis. Di SoundCloud kamu dapat merekam, mendownload dan mengunggah lagu serta berbagi catatan dengan pengguna lain.
Selain itu kamu juga dapat melihat rilis lagu terbaru dari artis terkenal, bahkan menemukan artis baru yg tidak terkenal sekalipun.
Namun bagi pengguna SoundCloud versi gratis hanya bisa mendengarkan musik mp3 secara online saja, bagi pengguna SoundCloud yang tidak menggunakan versi pro tidak bisa mendownload semua lagu di aplikasi resmi, kamu harus membayar SoundCloud Pro untuk mendapatkan fitur tersebut agar bisa download musik di Soundcloud tanpa dibatasi.
SoundCloud mengizinkan penggunanya untuk mendownload lagu yang tersedia secara gratis namun ada batasan untuk mendownload lagu berbayar di dalamnya.
Tapi tenang saja, karna pasti ada solusi atau cari lain untuk mendownloadnya tanpa harus membayar mahal-mahal membeli SoundCloud Pro. Di postingan ini Teknohits akan berbagi trik buat teman-teman di sini agar bisa mendownload musik dari SoundCloud secara gratis.
Trik yang akan Teknohits berikan ada 2 cara yang berbeda namun tetap sama menggunakan browser Chrome, cara ini tanpa software tambahan lagi. Jadi langsung saja mulai dari cara download lagu dari soundcloud yang pertama.
Download Lagu dari SounCloud Android atau PC : tanpa Aplikasi
1. Kunjungi situs SoundCloud.
2. Cari 1 lagu yang ingin kamu download.
3. Copy URL dari lagu tersebut, lihat gambar dibawah.

4. Selanjutnya klik tautan berikut 9SoundCloudDownloader.com.
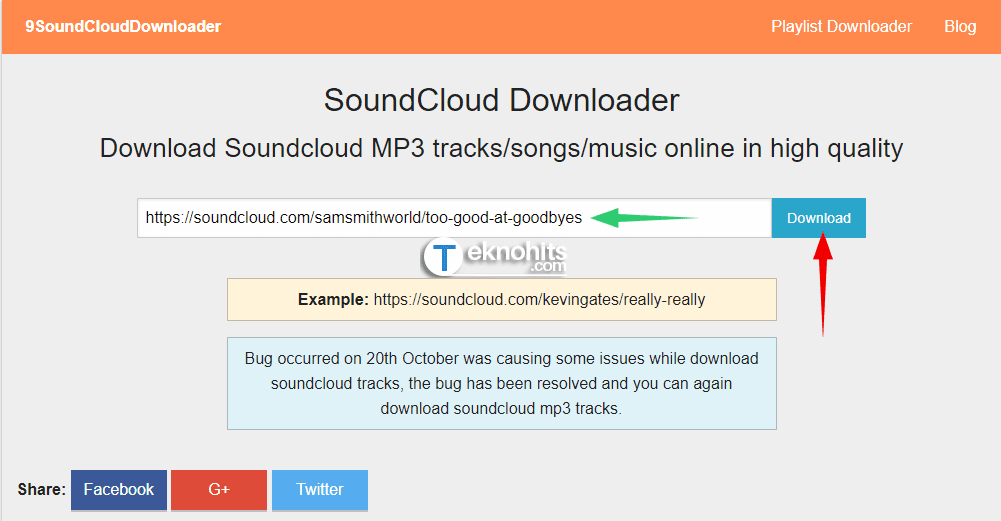
5. Paster URL lagu yang tadi kamu copy, paste url di kolom kemudian klik Download.
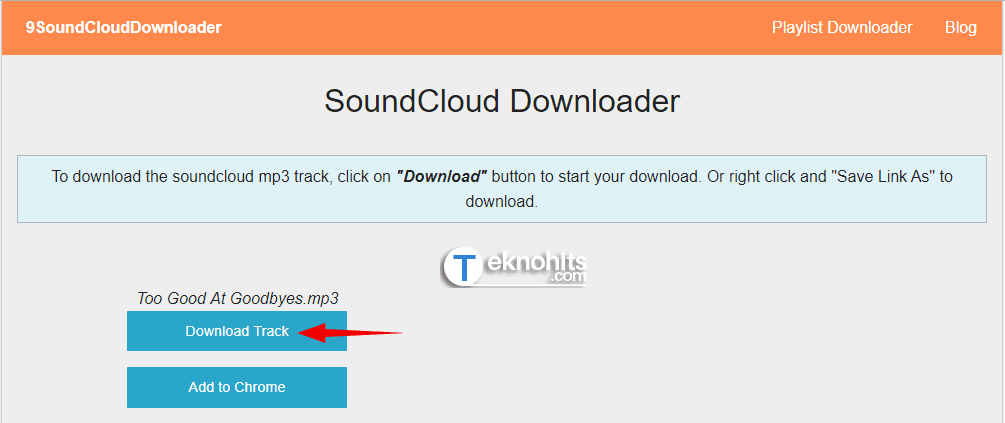
6. Langkah terakhir, klik tombol Download Track untuk menyimpan lagu format .mp3.
Download Lagu di SounCloud Menggunakan Ekstensi Chrome
Cara yang ke 2 ini lebih gampang dan cepat karena menggunakan ekstensi. Ekstensi ini tidak hanya mendownload lagu individual saja, tapi bisa juga mendowload daftar putar lagu SoundCloud hanya dengan 1 klik tombol saja, hebat bukan! itu karena ada fitur Downloading SoundCloud Playlists di ekstensi tersebut.
Oke langsung saja ikuti langkah-langkah cepat berikut.
1. Buka browser Google Chrome.
2. Install ekstensi Downloader berikut SoundCloud Downloader
3. Klik tombol ADD TO CHROME. Tombol tersebut berada di pojok kanan atas.
4. Klik lagi Add extension ketika diminta.
5. Jika sudah selesai install, kunjungi halaman SoundCloud.
6. Cari lagu atau daftar putar yang ingin kamu download.
7. Klik tombol Download. Tombol download berada di ujung barisan tombol Like, Repost, Share dan Add to Next up.
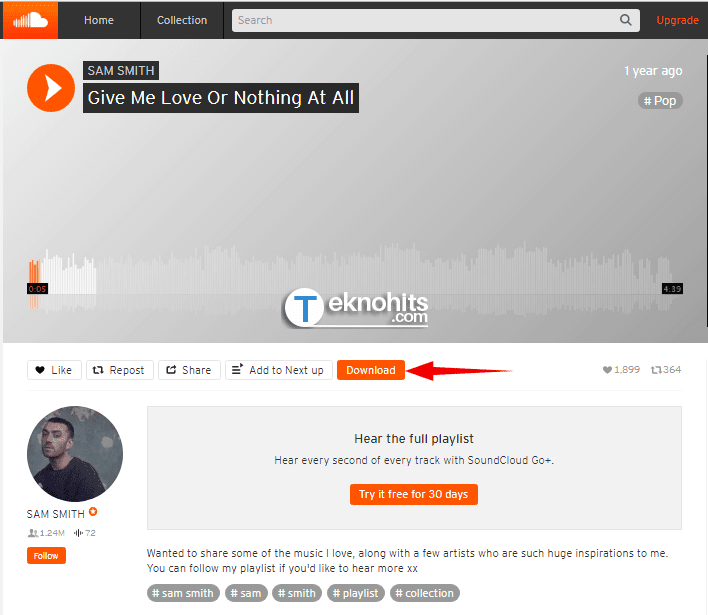
Catatan: Jika tombol download tidak muncul, coba teman-teman tutup browser google chomre dulu, kemudian buka kembali browsernya dan kunjungi lagi halaman SoundCloud. Setelah di refresh harusnya tombol download udah muncul.
Jika tombol download tidak muncul juga, teman-teman bisa pakai cara lain untuk mendownload lagu dengan ekstensi yang sama. Seperti gambar gif berikut ini.
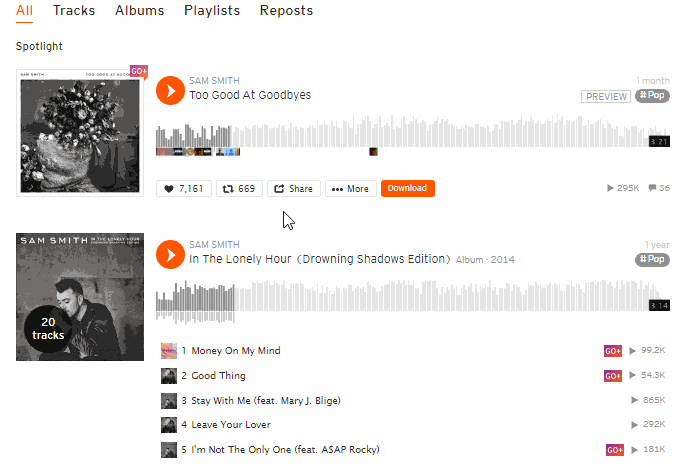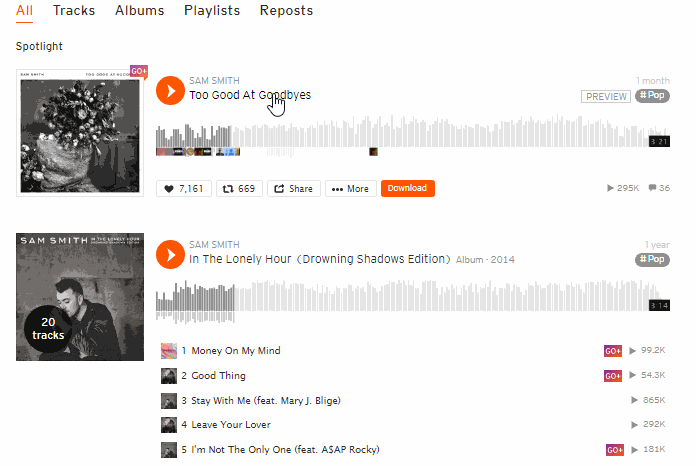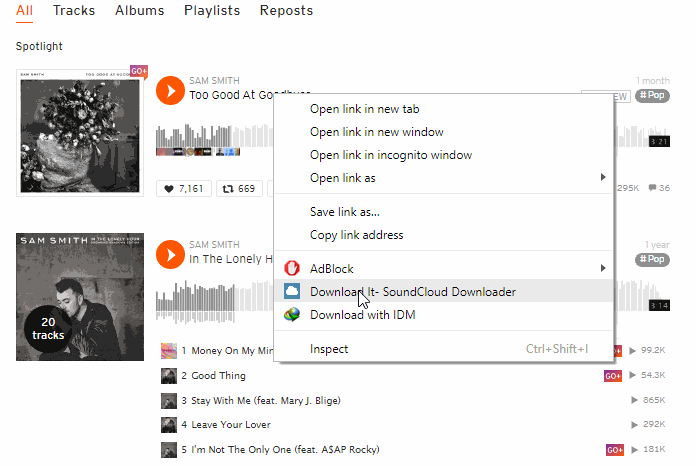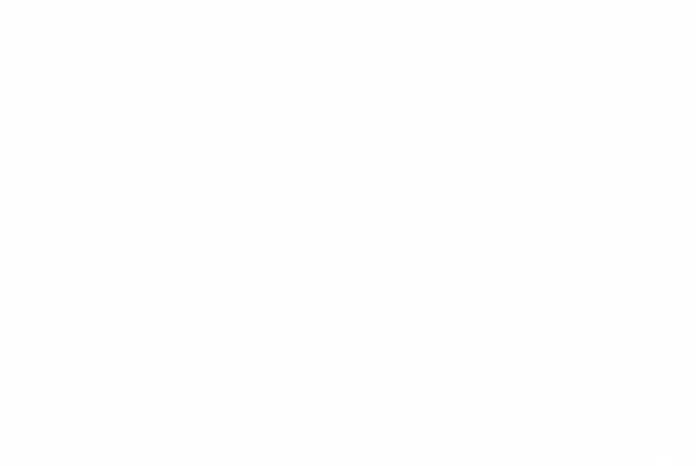
Setelah mengklik Download It-SoundCloud Downloader, kamu akan dialihkan ke tab baru. Di situ langsung saja klik DOWNLOAD THE SONG, lagu akan tersimpan otomatis ke folder download kamu.
Itulah 2 cara download lagu dari soundcloud tanpa perlu aplikasi tambahan lagi. Jika masih bingung dengan tutorial ini, kamu bisa bertanya di kolom komentar, kami akan membantu. Selamat mencoba!
Peringatan! Sebaiknya jangan download lagu secara ilegal. Belajar menghargai karya orang lain.
